AIで予測!身長300㎝の人の靴のサイズは?
突然ですが、世界で最も背の高い方は何㎝あるかご存じですか?🤔
記録上、最も背の高い人はアメリカ人のロバート・ワドローさんという方で、その身長は272cmにも達したそうです😲日本人男性の平均身長が170cmくらいと考えると1mも高いですね!
さて、今回は「もしも身長300cmの人がいたら、その人の靴のサイズは何センチになるか」という想像の答えを、AIのアルゴリズムを利用して予測してみたいと思います!
(ちなみにロバートワドローさんの靴のサイズは43cmだそうです)
今日使うAIのアルゴリズムは『回帰(かいき)』と呼ばれるもので、AIの予測アルゴリズムの中でも最もシンプルなものの1つです。少し解説が長くなりますが、最後までお付き合いください😁
回帰とは
データ(点)の集合から直線や曲線のグラフを引くことを指し、データが存在しない値でも新しく引いたグラフを見ればその値を予測することができるというものです。
![]()
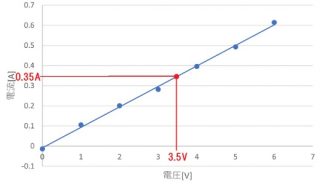
例えば、オームの法則の実験で得られた電圧と電流の関係を表すデータ(点)は離れ離れですが、ほぼ直線で結べます。
3.5Vの時の電流のデータは取っていませんが、新しく引いた直線から0.35[A]と分かりますね。
今回は回帰の中でも最もシンプルな、線形回帰(グラフが直線となるもの)を使っていきたいと思います📏
直線のグラフ y=ax
ここで復習ですが、直線のグラフはy=ax+bという方程式が表せます。aはグラフの傾きを表し、bは切片といって、x=0の時のyの値を言いますね。
特に、この直線が原点(x,y)=(0,0)を通るときは切片b=0となり、y=axとシンプルにできます。
身長が0cmであれば当然足のサイズも0cmになるので、今回は後者の方程式を使いましょう。
予測AIを作るために、人工知能学科の学生に協力してもらって身長と足のサイズを集計した散布図を作成しました。
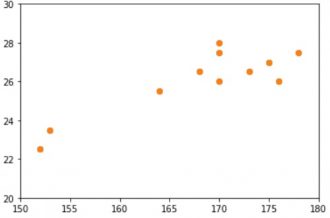
多少のばらつきはありますが、ある程度は身長と足のサイズは比例する関係にあるようです。
(両者の関係の強さを相関係数という数値で表しますが、ここでは割愛します)
それではここで、読者の皆さんに質問です!
上の散布図を見て、散らばったデータのところに直線を引いてみてください。直線なので、曲げたり折れたりしてはダメです!
人それぞれ差はあると思いますが、おおよそこのような線を引いたのではないでしょうか??
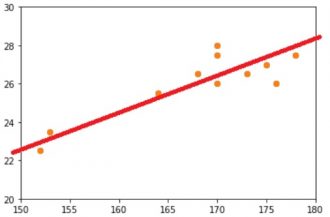
このような直線を手で引くのは簡単ですが、AIはコンピュータ上で動きます。そのためには、このグラフの方程式の中にある傾きaを計算して出す必要があります。そこで用いるのが『最小二乗法』です。
最小二乗法って?
まず、最小二乗法に用いられるデータとして二乗誤差というものがあります。二乗誤差とはy=axの直線とデータ点との距離を二乗したものです。
線形回帰では、二乗誤差を全データ分合計して、その値が最も小さくなるaを求めることになります。
説明のためにアニメーションを作ってみました。直線とデータの距離は青の線で表しており、右の帯が誤差の合計です。
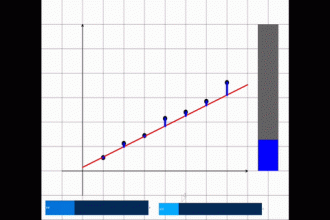
直線の位置や傾きを調整すると、誤差が変化します。離れれば離れるほど二乗誤差は大きくなりますね。
二乗誤差を最小化する
二乗誤差が最も小さくなるaを求めるには、二乗誤差を合計したり、それを微分したり、式変形したり、、、とっても大変ですので割愛します🙏
(高校数学で習う、極値の計算と近い仕組みです)
![]()
これによってaが得られたら線形回帰は完了です。
もうお気づきかも知れませんが、実際に測った身長と足のサイズのデータ(教師データといいます)を与えることでグラフの傾きaを求めるので、これは教師あり学習に分類されます。
では最後に、得られた直線から身長300cmの人の靴のサイズを予測しましょう。そうすると、、、
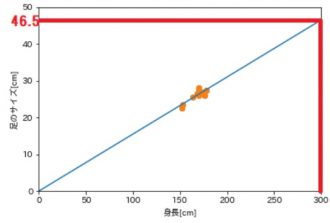
(教師データのところを拡大した図)
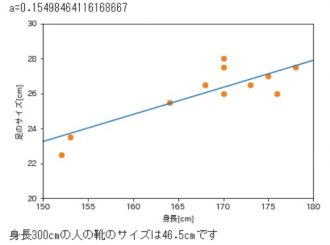
46.5cmという予測が得られました。パチパチ🙌
もちろん、教師データが変わればaの値も変わって予測結果は違う数字になると思いますが、272cmのロバートワドローさんの靴のサイズは43cmと考えるとまずまずの精度かと思います。
今回は線形回帰というとてもシンプルな予測AIを作ってみましたが、計算式自体は中々骨が折れます😭
しかし、AI開発で有名なPythonなどのプログラミング言語にはこれらの計算を簡単にやってくれるものがあるので、式が分からないからプログラムが書けないということはありません!
車がなぜ動くかを知らなくても、私たちは不便なく車を運転できるのと同じことですね。
ちなみに、グラフが線形ではなかったり、方程式がもっと複雑だったりと、まだまだたくさんのパターンがあります😨
そんな悩みをズバッと解決する『ニューラルネットワーク』・『ディープラーニング』についても紹介していきますのでお楽しみに!



